Derivatives arbitrage opportunities in India
Faculty Contributor: V. Ravi Anshuman, Professor
Student Contributors: Vikas Dugar and Sumit Sarda
The article investigates arbitrage opportunities in Indian cash and derivatives equity markets over the 6 months from November 2008 to April 2009 using three strategies – box spread, conversion-reversal and cash and carry arbitrage. While the study suggests that the Indian derivative markets are efficient, it also shows that they provide some arbitrage opportunities. We found that box spread provides more arbitrage opportunities than conversion-reversal; however, cash and carry arbitrage is more popular owing to its simplicity and quick trades. Among the transaction costs, Securities Transaction Tax (STT) forms the largest cost component and hence, a kind of spoilsport in arbitrage opportunities.
We were curious about the possibility and extent of arbitrage opportunities in equity cash and derivatives markets in the Indian capital markets. While exploring that, we also wanted to analyse the components of transaction costs and identify which component was the major contributor to the transaction cost. This article is a result of our primary research to find arbitrage opportunities in National Stock Exchange (NSE) cash and derivatives markets.
In this article, we will talk about our findings from out study starting with box spreads and then proceeding to transaction costs and their impact on box spread results. Application of conversion–reversal strategies, which combine a stock with the proxy of stock’s payoffs created using options on the same stock, will be covered next. The arbitrage opportunities in Futures will follow that. We will also highlight upon some arbitrage opportunities used in the real world by means of an interview with a trader.
Box Spread1
A box spread involves buying a bull spread and buying a bear spread.
A Bull Spread is created by buying a call option with a low exercise price and selling another call option with a higher exercise price (the Z-shaped payoffs of a call bull spread are shown in Exhibit 1). Alternatively, one can also create a bull spread using put options by purchasing one put option while simultaneously selling another put option with a higher strike price. A bull spread buyer expects asset price to rise.
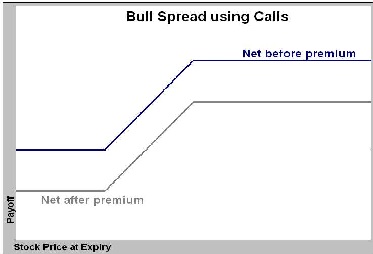 Exhibit 1: Payoff from a Bull Spread
Exhibit 1: Payoff from a Bull Spread
Doing converse of the above gives a Bear Spread, under which case the buyer of bear spread expects the prices to fall. Its payoff forms a mirror image of letter Z.
In an efficient world, a bull and bear spread on the same set of exercise prices should cancel the payoffs. However, in an inefficient market they do not, and leave the investor with a riskless profit. Since using call and put can create bull and bear spreads, we can create a box spread in two ways:
- Bull Box Spread: Long bull call spread and long bear put spread, or,
- Bear Box Spread: Long bear call spread and long bull put spread
Bull Box: Long Bull Call and Bear Put Spread2
A bull box-spread comprises of four options on the same underlying asset, with the same terminal date. Their pairings can be in two ways, as shown below (assume strike-prices K1 < K2):
- Long bull call spread: Buy a call option at K1; Sell a call option at K2
- Long bear put spread: Sell a put option at K1; Buy a put option at K2
Testing Bull Box on Reliance June Options Contracts. Bhav Copy as on June 15, 2009 (Assuming No Transaction Costs)
- Long bull call spread: Buy call at K1 = 2190 (@-87.6); Sell call at 2220 (@+75.6)
- Long bear put spread: Sell put at 2190 (@+89.2); Buy put at 2220 (@-105.35)
 Exhibit 2: P&L Payoff Matrix at Expiration
Exhibit 2: P&L Payoff Matrix at Expiration
As shown in Exhibit 2, this strategy gives a riskless profit of Rs 1.85 at any closing stock price.
Bear Box: Long Bear Call Spread and Long Bull Put Spread
Alternatively, doing the reverse can also create a bear box spread, i.e.
- Bear call spread: Short a call option at K1 and long a call option at K2
- Bull put spread: Long a put option at K1 and short a put option at K2
Testing Bear Box Spread on Reliance June Option. Bhavcopy3 as on June 15, 2009 (Assuming No Transaction Costs)
- Long bull call spread: Sell call at 2250(@+63.15); Buy call at 2310 (@-45.7)
- Long bear put spread: Buy put at 2250 (@-120.4); Sell put at 2310 (@+167.55)
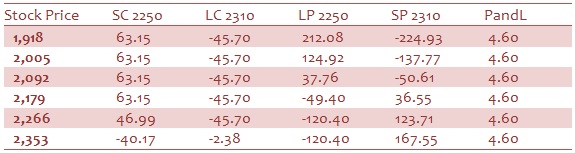 Exhibit 3: P&L Payoff at Expiration Matrix
Exhibit 3: P&L Payoff at Expiration Matrix
As shown in Exhibit 3, this strategy gives a riskless profit of Rs 4.6 at any closing stock price.
Summary of Further Tests
We tried different combinations of exercise prices for Reliance and NIFTY and found three arbitrage opportunities in Reliance (gain ranging from Rs 1.85 to Rs 4.5) and eight arbitrage opportunities in NIFTY (gain ranging from Rs 2.7 to Rs 10.85).
Transaction Costs
The above arbitrage gains were then subject to the following transaction costs, which can erode all or part of the gains. An arbitrage strategy is successful only if it can generate gains even after such transaction costs. As per our study of practices and regulations, we have the following types of transaction costs:
- Securities Transaction Tax (STT) - Depending on the instruments traded, STT charges may vary from 0.017% or 0.125%.
- Interest - We assumed interest cost at the rate of 1.5% per month for funding the upfront payment of premium or margin money or proceeds to buy a stock.
- Brokerage (including Service Tax) - Market usually charges brokerage at the rate of 0.01% of exercise price and service tax at the rate of 12.5%. In case the person carrying out the arbitrage strategy is a broker himself, he will save this cost.
- Interest on Margin Money - Option writer has to pay margins to the extent of 10-20% of Exercise price. No margin requirement exists in the case of an option buyer. We have taken the interest @1.5% per month as transaction costs.
Impact of Transaction Costs on above Strategies
Transaction costs, particularly STT, eroded most of the gains. However, a few strategies could still generate gains even after these costs. Exhibit 4 shows a summary of the payoffs.
 Exhibit 4: Specimen box spread gain
Exhibit 4: Specimen box spread gain
Box Spreads
Bear box spread will normally show higher net gains because it generates net premium income in the hands of the arbitrager. However, to be conservative, we have not taken interest income on this premium receipt.
Testing Bull Box on Combinations of All Nifty Options Contracts after taking Transaction Costs (November 2008 to April 2009)
Exhibit 5 denotes the number of arbitrage opportunities that existed after considering the above transaction costs on all the NIFTY options combinations with a minimum volume of 100 contracts per day between November 2008 and April 2009.
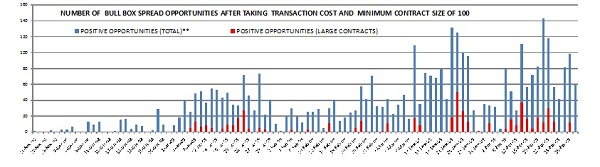 Exhibit 5: Number of Bull Box arbitrage opportunities after transaction costs for minimum 100 contracts
Exhibit 5: Number of Bull Box arbitrage opportunities after transaction costs for minimum 100 contracts
Testing Bear Box on Combinations of All Nifty Options Contracts after taking Transaction Costs (November 2008 to April 2009)
Exhibit 6 denotes the number of arbitrage opportunities that existed after considering the above transaction costs on all the NIFTY options combinations with a minimum volume of 100 contracts per day between November 2008 and April 2009.
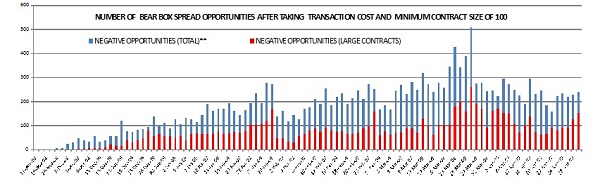 Exhibit 6: Bear Box spread arbitrage opportunities in all combinations of NIFTY for minimum 100 contracts
Exhibit 6: Bear Box spread arbitrage opportunities in all combinations of NIFTY for minimum 100 contracts
Inference: Bear box strategies tend to throw more arbitrage opportunities.
Rationale: The arbitrager received a net premium in case of bear box spread and hence, we can save the interest costs on net premiums.
Conversions and Reversals4
Conversion and reversal strategies create synthetic stock payoffs, which should be identical to actual stock. In case it is not identical to actual stock, there arise arbitrage opportunities.
Conversions
Payoffs from a long position stock can be synthetically created using options by buying a call and selling a put of the same exercise price. Ideally, net payoff from a portfolio of a long stock and synthetic short stock should be zero. If it is not zero, there exists an arbitrage opportunity by:
- Longing a stock
- Shorting a call
- Longing a put
This is the conversion strategy.
Testing Conversions using Reliance June Contracts; Bhavcopy3 as of June 15, 2009
- Long Reliance stock @ -2179
- Short Reliance June call 2190 @+87.6
- Long Reliance June put 2190 @ -89.2
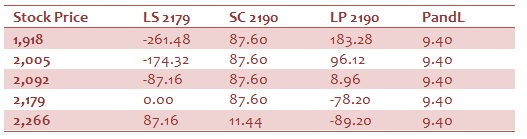 Exhibit 7: PandL Payoff at Expiration Matrix
Exhibit 7: PandL Payoff at Expiration Matrix
Conversion strategy leads to net payoff of Rs 9.4 (Exhibit 7) irrespective of actual stock price.
Reversals
On lines similar to bear box spread, there can be a reversal strategy (antithesis of conversion). We can change all the loss-making conversions to reversals by
- Shorting the stock
- Longing the call
- Shorting the put
A reversal is the opposite of conversion. One can make arbitrage gain in an overpriced stock. As an example, consider the following portfolio:
- Long Reliance stock @ -2179
- Short Reliance June call 2190 @+87.6
- Long Reliance June put 2190 @ -89.2
Summary of Further Tests on Conversions
We tried different conversion strategies for various combinations of exercise prices for popular stocks and found 4 arbitrage opportunities in Reliance, 5 arbitrage opportunities in Reliance Natural Resources Limited (RNRL) and 2 arbitrage opportunities in National Thermal Power Corporation (NTPC).
The following depicts a specimen strategy (using Reliance bhavcopy3 as on June 15, 2009) that gave positive payoffs after considering transaction costs.
- Exercise Price= Rs.2250
- Gross Arbitrage Gain= Rs.13.75
- Transaction costs= Rs.12.59
- Net Gain= Rs.1.16
Following graph (Exhibit 8) denotes the number of arbitrage opportunities that existed after considering the above transaction costs for carrying minimum contract sizes (20).
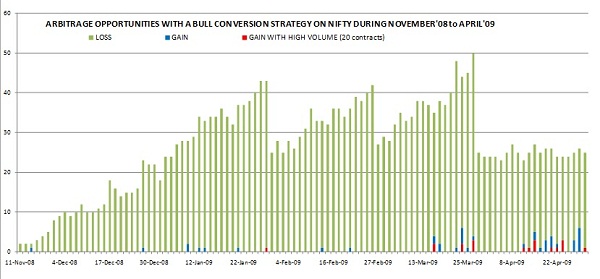 Exhibit 8: Number of arbitrage opportunities in all combinations of NIFTY contracts for minimum 20 contracts
Exhibit 8: Number of arbitrage opportunities in all combinations of NIFTY contracts for minimum 20 contracts
A comparison of box arbitrage and conversion arbitrage thus shows that number of opportunities is more in box arbitrage than in conversion arbitrage.
Cash and Carry Arbitrage in Futures5,6,7
The forward price represents the expected future value of the underlying asset discounted at the risk free rate. Thus, for a simple, non-dividend paying asset, the value of the future/forward, F(t), will be found by compounding the present value S(t) at time t to maturity T by the rate of risk-free return r.
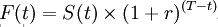
We can modify this relationship for storage costs, dividends, dividend yields, and convenience yields. We looked for instances where this ideal pricing principle was not met and which could be exploited as an arbitrage.
We compared the futures price and the spot prices of reliance under the following assumptions:
- The risk free rate is 3.5%
- The interest free margin payable on future trade is 50%
- The STT is payable only by the seller and not by the buyer
- We already own/ hold the underlying security (stock) equal to one lot size of futures contract
We observed a possibility of making a risk free profit by
- Selling the stock short
- Investing the proceeds into risk free securities
- Going long on the Stock futures (with no STT payments)
-
- Utilising the proceeds from the Risk free securities to purchase the stock after the expiry of the futures contract at the futures price
Testing for Reliance stock
For the stock under Review (Reliance) for the period 1-May-2009 to 30-Jul-2009, we observed the following profit opportunities (Exhibit 9) by following the above strategy:
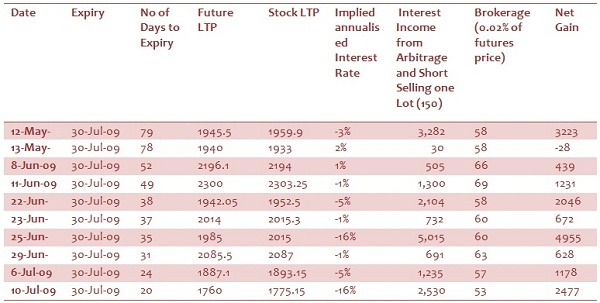 Exhibit 9: Net arbitrage gain for Reliance cash and carry arbitrage
Exhibit 9: Net arbitrage gain for Reliance cash and carry arbitrage
Real World Practices – Interview with Arbitrage Trader
We interviewed one of the partners of a pure arbitrage firm, operating in Mumbai. We enquired him on the real world arbitrage practices. The most often-used arbitrage strategy by this arbitrage firm is between cash and carry and reverse cash and carry. This was owing to the simplicity in carrying out trade. Option strategies needed multiple instruments to construct the trades.
Conclusion
As per the study, while the Indian derivative markets are efficient, however, they do provide some arbitrage opportunities. Among option arbitrage strategies, Box spread arbitrage strategies tend to give more opportunities than the conversion/reversal arbitrage strategies. As regards the Futures market strategies – price differential between cash and futures market, interviews with traders and arbitragers showed that most of the arbitrage play in India is concentrated on the largely traded future contracts such as Nifty and Reliance. Among the transaction costs, STT (Security Transaction Tax) forms the largest cost component and hence, a king of spoilsport in arbitrage opportunities. This could possibly be one of the reasons, why there was a resounding demand in the Union Budget (2009) to scrap STT.
Keywords
Finance and Control, capital markets, derivatives, futures, options, India, arbitrage, box spread, bull spread, bear spread, conversion, reversal, cash and carry arbitrage, transaction costs, securities transaction tax
Contributors
V. Ravi Anshuman is a professor in the Finance and Control area at IIM Bangalore. He is Bachelor of Technology (Mechanical Engineering) from IIT Kharagpur and holds a Ph D Finance from University of Utah, USA. He can be reached at anshuman@iimb.ernet.in.
Vikas Dugar (IIMB, PGP 2008-10) is a Chartered Accountant and Chartered Financial Analyst and can be reached at vikas.dugar08@iimb.ernet.in.
Sumit Sarda (IIMB, PGP 2008-10) is a Chartered Accountant and Company Secretary and can be reached at sumit.sarda08@iimb.ernet.in.
References
- Lawrence G. McMillan, 2004, “McMillan on Options”, John Wiley and Sons, Inc., Hoboken, New Jersey, pp 1-104
- Lawrence G. McMillan, 2002, “Options as a Strategic Investment”, New York Institute of Finance Publication, 1330 Avenue of the Americas, New York, pp 172-190, 271-288, 321-333, 422-455
- Website of the National Stock Exchange, http://www.nseindia.com/
- Martin J. Pring, 2002, “Study Guide for Technical Analysis Explained”, McGraw-Hill, Two Penn Plaza, New York, pp 3-135
- David A. Dubofsky and Thomas W. Miller, 2002, “Derivatives: Valuation and Risk Management”, Oxford University Press, Walton Street, Oxford, pp 347-559
- Scott H. Fullman, 1992, “Options: A Personal Seminar”, New York Institute of Finance Publication, pp 183-193
- London International Financial Futures and Options Exchange (LIFFE) Administration and Management, Cannon Bridge House,1 Cousin Lane, London EC4R 3XX, United Kingdom 2002, “LIFFE Options: A guide to Trading Strategies”, pp 1-71, http://www.euronext.com/fic/000/010/729/107297.pdf
