Study of Real Market Forces Influencing Volatility Skew Curves
Faculty Contributor : V. Ravi Anshuman, Professor
Student Contributors : Kamal Choudhary and Kapil Shashi Choudhary
Volatility skew curve is a plot of the strike prices against the implied asset price volatility for options with similar characteristics. It is usually skewed downwards for equities. However, for Indian stocks, there are deviations from this, leading to arbitrage opportunities. This article analyzes the reasons and extent of such opportunities across various industries. The primary reason for such deviations is low liquidity. Other reasons include a higher worldwide demand for puts, inflation of mutual funds’ NAVs (net asset value) at the end of the month and OTC (over the counter) trading by institutional investors. Also, deviations are higher for high market capitalization companies and sectors due to the higher systematic risk associated with them.
Introduction
In a Black-Scholes world, given the market price of an option and various other parameters, the Black-Scholes formula can be used to calculate the implied volatility of a stock. In the real world, there is a different implied volatility for each strike and maturity price. One can interpret it as the market’s expectation of future volatility between today and the maturity date in the scenario implied by the strike price. For instance, out-of-the-money puts are natural hedges against a market dislocation (such as the recession caused by the recent financial crisis) which entails a spike in volatility; the implied volatility of out-of-the-money puts is thus higher than in-the-money puts.
Further, as per put-call parity, European calls and puts with identical characteristics must have the same implied volatility. Hence, in a plot of implied volatility against strike price, the curve is typically downward sloping. This phenomenon is known as the volatility skew and has been clearly observable especially after the 1987 US market crash. In the absence of a volatility skew, a number of arbitrage opportunities may result. This article explores the presence of volatility skew in the Indian market.
Methodology
We tested the presence of volatility skew in various Indian stocks across three different sectors using historical price data and the Black-Scholes model. Exhibit 1 illustrates the methodology used to generate skew curves from relevant strikes. The industries and stocks under consideration were Information Technology (IT) – Infosys and Tata Consulting Services (TCS), Oil and Gas – Reliance Industries and Oil and Natural Gas Corporation (ONGC), and steel – Tata Steel and Steel Authority of India (SAIL).
The aim was to consider options expiring in May 2009 and May 2008 at different times (30 days, 20 days and 10 days) to maturity. However, the liquidity in some of these situations was too low to warrant any meaningful analysis (in spite of choosing stocks with highest liquidity) and thus we left it out of analysis. We consider the one-month MIBOR rate as the risk free interest rate.
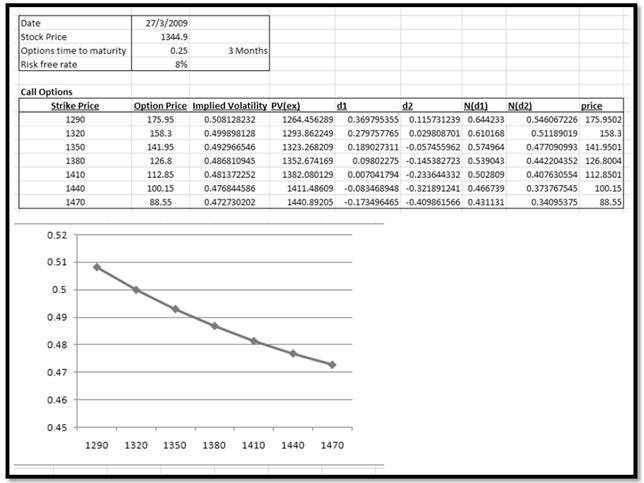 Exhibit 1 Methodology for computation of Volatility Skew curve using call options in relevant range of strike prices
Exhibit 1 Methodology for computation of Volatility Skew curve using call options in relevant range of strike prices
Observations from the Volatility Skew Analysis
The volatility skew analysis leads to a number of general observations:
- There is extremely low liquidity in the Indian stock option market. For example, 30 days before expiry, a total of only 143 call option contracts and 95 put option contracts were traded in a day across all the strikes even for a highly liquid well reputed stock like Infosys.
- Liquidity was considerably lower in May 2008 as compared to May 2009 indicating a slow, but definite improvement.
- Trading was comparatively higher in at-the-money and out-of-the-money options as opposed to in-the-money options.
- Implied volatility increases in magnitude and is also itself more volatile as the option approaches maturity due to higher trading volume near maturity.
- One of the reasons for this is that people close out their open positions near maturity.
- Also, apparently, Indian investors prefer to speculate on and hedge against near options as opposed to far options. This may be due to high volatility in the stock market, primarily due to the recession, resulting in the market being so unstable that the investors are unable or unwilling to predict far into the future.
We now look at some interesting observations in various stocks.
Observations in Infosys stock
- In 2009, the call option volatility was slightly higher than the put option volatility at the same strikes. This was primarily due to greater trading volume in call options. However, a different implied volatility for the same strike implies clearly that put-call parity does not hold and thus there is an arbitrage opportunity.
- In 2008, because of the lower liquidity, the observations were much more unpredictable. An unusual situation was that trading volume actually decreased as the option neared maturity and thus the results were unexpected.
Observations in Reliance Industries stock
- The difference between put and call volatilities reduced significantly with decrease in time to expiration and increase in trading volume.
- Of all the stocks considered, Reliance shows the largest amount of liquidity change from 2008 to 2009. It is observed that for the same strikes, there is only a minor difference between the call and put volatilities with the put option having slightly higher volatility.
Observations in Tata Steel stocks
- Contrary to the expectation of volatility, most of the implied volatilities increase with strike price. Thus, in effect, the lower strike options of Tata Steel are underpriced (a low implied volatility implies low option price) as opposed to higher strike options.
- Option volatilities increase significantly with decreasing time to expiration probably due to higher trading volume.
- The put option has a significantly higher volatility than the call option resulting in an absence of put-call parity which leads to a significant arbitrage opportunity.
Findings and Recommendations
From the detailed analysis of volatility skews of various stocks across industries, it is apparent that clear arbitrage opportunities exist in the market due to differences in implied volatilities of call and put options. In most cases, we concluded that put implied volatilities were higher than call implied volatilities resulting in violation of put-call parity. We analyzed the reasons behind the existence of such arbitrage opportunities and what stops traders from exploiting them in the real world. Interactions with volatility traders led to the discovery of a number of practical reasons, which are unaccounted for in the theoretical world of Black-Scholes.
Role of Liquidity
The lack of liquidity in the stock options market can create differences in put and call implied volatilities leading to violation of put-call parity. To test this hypothesis, we analyze the impact on the difference in implied volatilities of puts and calls with changes in liquidity. The analysis resulted in the observation of following trends.
- The liquidity in the options market is very low in the first few days of trading and increases as options approach maturity.
- Liquidity has improved from 2008 to 2009, but trades with time to maturity greater than 30 days are still essentially restricted to only a few institutional investors.
There are conflicting results when liquidity is compared with difference in implied volatilities.
- The difference in call and put implied volatilities tends to reduce in last 5-10 days of trading for stock options as the liquidity situation improves. This substantiates the role of liquidity.
- However, liquidity has increased from 2008 to 2009 liquidity, and hence the magnitude of difference in implied volatilities should have reduced. But instead it has increased. A possible reason is that overall base volatility has increased in 2008-09 due to worldwide financial crisis.
Hedging - Put versus Call implied volatility
Demand and supply differences explain a higher put implied volatility. In general, worldwide trading of put options tends to be relatively higher than call options due to the use of put based hedging strategies to hedge against a sizable downward movement in the stock market. Thus, due to higher put option demand, investors are willing to pay a relatively higher premium for put. High-implied volatility of put options reflects the high premium. However, while worldwide ratio in trading volumes is of the order of 3 to 1, the ratio is only 1.5 to 1 in India. Thus, in India, this factor is clearly not the most significant factor when accounting for the huge difference in call and put implied volatilities.
Role of Mutual Funds: Hijacking NAV
Another possible explanation for higher put implied volatility is that the Indian mutual funds try to inflate their net asset values (NAV) temporarily, towards the end of a month. One way to do this is to increase cash in the fund. Therefore, they start writing many put options, which serve a dual purpose of hedging against market dislocation and getting extra cash into the fund as a premium for writing these options. To test this hypothesis, we analyzed NAVs of three mutual funds and observed a small rise in their NAVs towards end of month.
Market Prices versus Real Prices
Another interesting explanation is that institutional investors, who generally trade in high volumes, do not trade at fair market prices. These traders need to instantaneously trade relatively high volumes and cannot wait for orders to be placed in the NSE (National Stock Exchange) order book. Hence, they directly call up their counter parties in one of the Mutual Funds.
Both parties calculate their own fair values separately and then negotiate on a common price. Then, both the parties call their dealers registered with NSE and ask to enter the two orders, where they will instantly match against each other. As a result, normal retail stock investors rarely get to trade with big financial institutions and end up paying a relatively higher premium for their trades. Thus, market prices are relatively higher which results in higher implied volatility.
In other words, this implies liquidity issues do not greatly restrict the financial institutions as they rarely trade with retail investors. However, the retail investor has to pay a premium to participate in those trades, which result in higher market prices.
Implied Volatilities across Industries
Across industries, our observations found significant variations in the extent of arbitrage opportunities. Difference in implied volatilities of call and put options is very high in some industries like oil & gas and steel as compared to other industries like IT. This is possibly due to the relatively low beta and high market capitalization of few industries and firms.
In nonprofessional terms, if RIL, ONGC, or Tata Steel is going to go down, it means that not just these but the whole market will go down. These companies contribute towards the systematic risk. Thus, to hedge against such market crashes or large dislocations, the investor is willing to pay a higher premium and thus there is a larger difference between put and call implied volatilities in these industries as the purpose of puts is for hedging. On the other hand, if companies in IT sector go down, the rest of the market need not follow suit. Systematic risk affects these companies, but their contribution to systematic risk is relatively less. Thus, the investor does not pay high premium for these companies, resulting in their lower prices and lower implied volatilities.
Conclusion
The most significant conclusion from cross-industry volatility skew curve analysis is that the Indian stock options market is very different from the perfect theoretical world of Black-Scholes. A number of factors linked to behavioural finance, incentives for managers, and monitoring & regulatory limitations have a significant impact in the market price determination of options. As a result, there are a number of market imperfections. Some of these imperfections result in consistent predictable deviations from theoretical models, which one can adjust for in pricing models. However, a number of them, such as NAV inflation by mutual fund managers, result in change in shape of skew curves & isolated reversals, which violate some basic financial assumptions. Thus, overall, the Indian stock option market has a long way to go before it can reach the stability of option markets in developed countries.
Keywords
Finance and Control; Finance; Stock Markets; Variance Swaps; Volatility Skew; Volatility Smile; Arbitrage opportunities; Real market conditions; Replication
Contributors
V. Ravi Anshuman is a Professor in the Finance & Control Area at IIM Bangalore. He holds a Ph.D. in Finance from University of Utah and a Bachelor's degree in Mechanical Engineering from IIT Kanpur. He can be reached at anshuman@iimb.ernet.in
Kamal Choudhary (PGP 2008-10) holds a B.Tech. degree in Information Technology from the Indian Institute of Information Technology, Allahabad. He can be reached at kamal.choudhary@gmail.com
Kapil Shashi Choudhary (PGP 2008-10) holds a Dual Degree (B.Tech. & M.Tech) in Mechanical Engineering from the Indian Institute of Technology, Bombay. He can be reached at k_choudhary@yahoo.com
